풀이
삽입정렬은 카드놀이에서 새로운 카드를 받았을 때, 원래 갖고 있던 정렬된 배열에 새로운 카드를 정렬시켜 넣는 것에 비유할 수 있다.
기존 정렬된 배열의 맨 끝요소와 새로운 요소를 비교하는 방식으로 정렬을 진행한다.
예를 들어 [2, 3, 5, 7]의 배열이 있고, 추가로 [1]을 넣어준다면 7과 1을 비교해서 1이 더 작으므로 7의 index 위치에 1을 삽입하고, 7은 한칸 뒤로 미는 방식이다. 새로 넣어준 1이 정렬된 배열에서 제자리를 찾아갈 때까지 이 과정을 반복한다.
다만, 받아오는 배열은 전체가 정렬되지 않은 배열로 간주하고, 맨 첫번째 요소만 정렬된 것으로 생각하여 순차적으로 정렬과정을 진행한다.
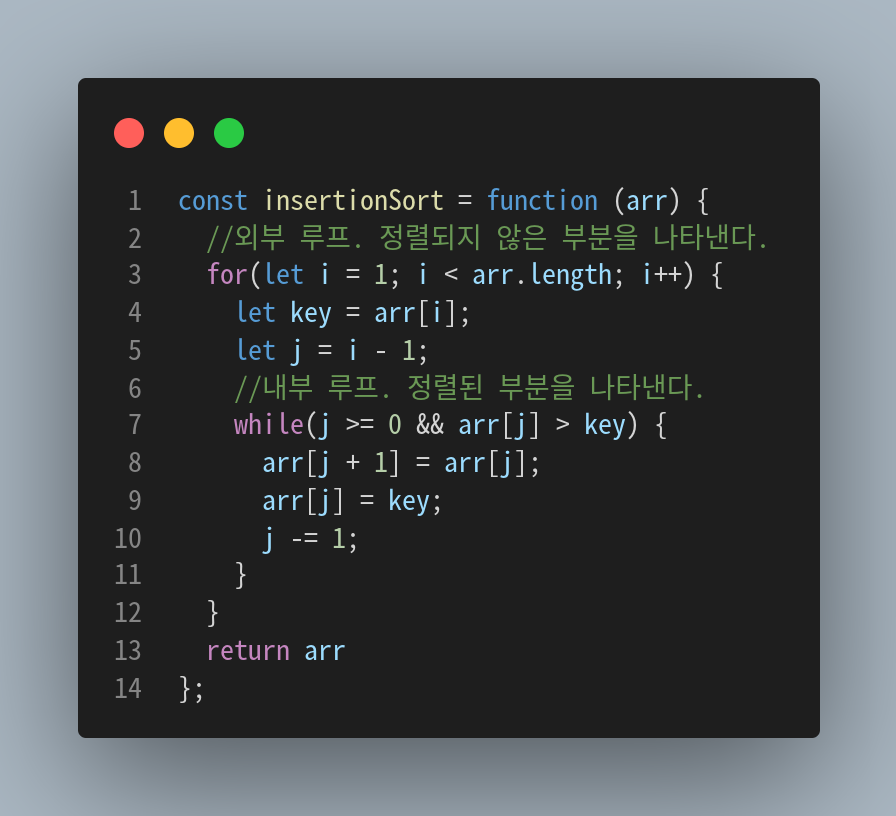
알고리즘 구현
알고리즘 구현은 정렬되지 않은 부분을 외부 루프로, 정렬된 부분을 내부 루프로하여 작성된다. 이해하기가 그리 어렵지 않은 방식이다.
배열에서 맨 처음 값 i = 0인 부분은 정렬되어 있다고 가정하고 i = 1에서부터 시작한다.
새로 삽입할 값(판단할 값)을 key = arr[i]로 지정한다.
let j = i - 1에서부터 이미 정렬된 값들과 key값을 비교하여 key값을 정렬된 배열에 삽입한다.
시간복잡도
최악의 경우는 완전히 반대로 정렬되어 있는 경우이다. 각 외부루프의 단계에서 i번씩 원소들을 뒤로 밀어주어야 한다. 따라서 1+2+...+(n-1)이 되는 방식이므로 O(N^2)의 시간복잡도를 갖는다.
최선의 경우는 정렬되어 있는 경우다. 외부루프가 1, 2, ... , n번째까지 n-1번 이루어지는 동안, 비교(arr[j] > key)가 1번 이루어지므로 비교는 n-1번, 이동(arr[j + 1] = arr[j], arr[j] =key)이 2번 이루어지므로 총 2 * (n -1)번 이루어 지게된다. 따라서 O(N)의 복잡도를 갖게 된다,
'Computer Science > Algorithm' 카테고리의 다른 글
| 소수 구하기 : isPrime, prime number, sqrt (0) | 2021.01.09 |
|---|---|
| Prm 14 : rotatedArraySearch / binarySearch, 경우의 수 (0) | 2021.01.08 |
| Prm 11 : powerSet (0) | 2021.01.05 |
| Prm 10 : BinarySearch (0) | 2021.01.05 |
| Prm 9 : power / recursion (0) | 2021.01.04 |



