[패캠강의]이산수학 - ch3. 함수, 수열과 관계 : 부분 순서 관계, 곱집합 등

1. 함수

 

정의

집합 A, B에 대하여 모든 집합 A의 원소에 대하여 집합 B의 원소가 하나씩 대응될 때 A에서 B로 가는 함수 f라고 한다.

f: A -> B 라고 표기한다.

정의역 : f가 정의된 집합 A

공역 : B

치역 : { b | ∃ a ∈ A, f(a) = b}

 

 

함수 종류

 

• 일대일 함수(단사 함수) : 정의역의 모든 원소들이 서로 다른 공역의 원소와 대응하는 함수
• 전사 함수 : 공역과 치역이 일치하는 함수
• 일대일 대응함수(전단사함수) : 일대일 함수 중에서 공역과 치역이 일치하는 함수

 

---

 

2. 수열

 

함수 중에서 정의역이 자연수의 부분집합인 함수

 

 

 

---

 

3. 관계

 

두 집합 또는 집합의 원소간 관계를 다룬다. 여기서 특히 cartesian product 같은 경우에는 sql문에서도 나오는 개념이다.

 

순서쌍과 곱집합

 

순서쌍(ordered pair)

어떤 원소 a ∈ A, b ∈ B에 대하여 (a, b)와 같이 순서를 가진 쌍을 순서쌍이라고 하며 a를 첫 번쨰 원소, b를 두 번째 원소라고 한다.

 

곱집합(cartesian product)

공집합이 아닌 임의의 두 집합 A, B에 대해 a ∈ A, b ∈ B인 모든 순서쌍 (a, b)를 모아놓은 집합. A X B로 표기한다.

 

곱집합의 크기

유한 집합 A, B에 대해 | A X B | = | A | X | B | 이다.

 

 

이항관계(binary relation)

 

집합 A, B에 대하여 A에서 B로의 관계 R 은 A X B의 부분집합으로 정의된다. 이 때, (a, b) ∈ R 이면 a는 b에 대하여 R의 관계에 있다고 하며 a R b로 표기한다.

 

R에 속한 순서쌍 중 첫 번째 원소만 모아놓은 집합이 R의 정의역, 두 번째 원소만 모아놓은 집합이 치역이며 집합 B가 공역이 된다.

 

함수는 관계의 특수한 형태이다. f의 정의역이 A 전체이고, a ∈ A에 대하여 a R b를 만족하는 b ∈ B가 단 하나만 존재하는 관계를 함수라고 한다.

 

수열 < 함수 < 관계 로 포함관계가 정의되었다. 이렇게 계층적인 구조를 갖고 있으면 제일 큰 단위에서 무엇인가가 증명되면 하위 계층은 자동으로 증명되므로 수학은 이러한 계층 구조를 잘 정의한다.

 

관계는 아래와 같은 표현법들로 표현할 수 있다.

 

 

관계 종류

 

(1) 모든 원소 x ∈ X에 대해 (x,x) ∈ R이 성립하면 반사(reflexive) 관계라 한다.

(2) 모든 순서쌍 (x,y) ∈ R에 대해 (y,x) ∈ R도 성립한다면 대칭(symmetric) 관계라 한다.

(3) 모든 순서쌍 (x,y) ∈ R에 대해 x, y가 서로 다를 경우 (y,x) ∈! R이면 반대칭(antisymmetric) 관계라 한다.

(4) (x,y) ∈ R, (y,z) ∈ R이 성립하는 모든 x,y,z ∈ R에 대해서 (x,z) ∈ R도 만족한다면 추이(transitive) 관계라 한다.

 

위 행렬 그림에서 (1,2), (2,1) 부분을 비교했을 때, 둘의 결과값이 같으면 대칭, 다르면 반대칭 관계라고 보면 된다.

(1,2)가 관계를 갖고(1), (2,3)도 관계를 갖는데 (1,3)도 관계를 갖는다면 추이 관계이다. 예를 들어 R = {(a,b), (d,a), (a,a), (a,b)}인 경우 (d,a)와 (a,b)가 있기 때문에 (d,b)가 있어야 되는데 없으므로 추이 관계가 아니다.

 

집합그림으로 살펴보면 아래와 같을 것이다.

 

 

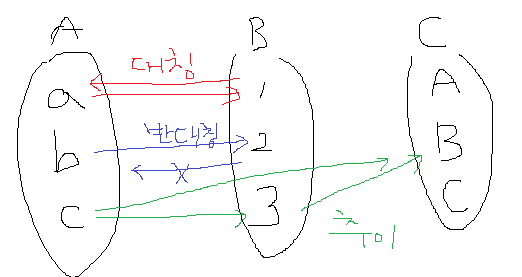
부분 순서 관계(Partial Order)

 

반사, 반대칭, 추이 관계가 성립할 때를 부분 순서 관계라고 한다. 반대칭 관계를 주목해보면 (b,2)는 있는데 (2,b)는 없다는 뜻이므로 위 집합그림에서 관계의 첫 번째 원소가 정해지면 두 번째 원소는 첫 번째 원소를 바라볼 수 없게 된다. 다시 말해 순서가 확정되는 형태이다. 그래서 부분 '순서' 관계라고 표현하는 것 같다.

 

부분 순서 관계는 집합의 포함관계로 나타낼 수 있다. 즉 부분 순서 관계는 집합 간의 일방적 순서 관계를 표현할 수도 있다. (하나의 예시일뿐 모든 부분 순서 관계가 이런 것은 아님)

 

 

비교가능(Comparable)/비교불가능(Noncomparable)

 

우선 순위를 판별 가능 여부에 따라 나눈다. 집합 A에 대한 관계 R이 부분 순서 관계이고, a < b 또는 b < a 이면 a와 b는 비교 가능이라고 하고, a ＜! b 또는 a >! b 이면 비교 불가능이라고 한다.

 

완전순서(Total Order)

 

집합 A에 대한 부분순서관계 R에서 집합 A의 모든 원소의 순서쌍을 비교할 수 있으면 관계 R을 완전 순서 관계라고 하며, 집합 A를 완전순서집합이라고 한다.

 

---

참조

 

1. 패스트 캠퍼스 - 한 번에 끝내는 컴퓨터 공학 전공필수 & 인공지능 심화 초격차 패키지 Online.

Part2. 이산수학 - 강승현 강사님