1. 문제
You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).
Find two lines that together with the x-axis form a container, such that the container contains the most water.
Return the maximum amount of water a container can store.
Notice that you may not slant the container.
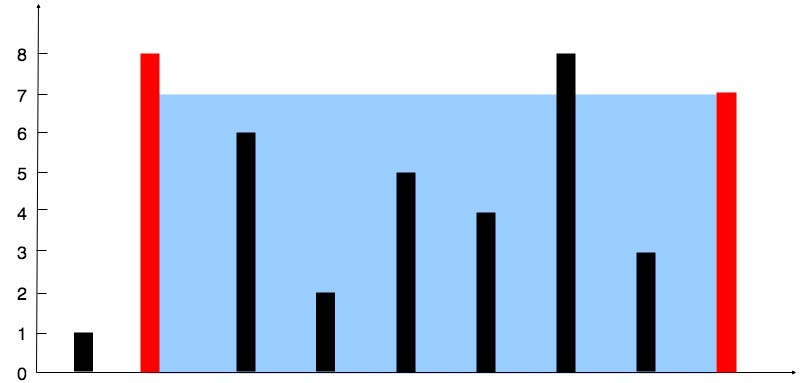
Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Input: height = [1,1]
Output: 1
Constraints:
- n == height.length
- 2 <= n <= 105
- 0 <= height[i] <= 104
2. 배운점
파이썬에서 index를 가지면서 for문을 거꾸로 돌리고 싶다면, 아래처럼 enumerate, list, reversed를 함께 활용하면 된다.
for idx2, h2 in reversed(list(enumerate(height))):
print(id2, h2)3. 내 풀이
풀이1
처음엔 좌, 우측 기둥을 고민하다가.. 나중엔 그냥 각 기둥사이별 모든 면적을 다 구한다음 최대값만 리턴해주었다. Greedy 알고리즘 방법을 적용한 것이다.
- time limit에 걸려서 테스트를 통과하지 못했다.
class Solution:
def maxArea(self, height: List[int]) -> int:
areas = [0]
def get_area(post1: Tuple[int, int], post2: Tuple[int, int]):
areas.append(abs(post2[0] - post1[0]) * (min(post1[1], post2[1])))
for i, post1 in enumerate(height):
for j, post2 in enumerate(height):
get_area((i, post1), (j,post2))
return max(areas)
풀이 2
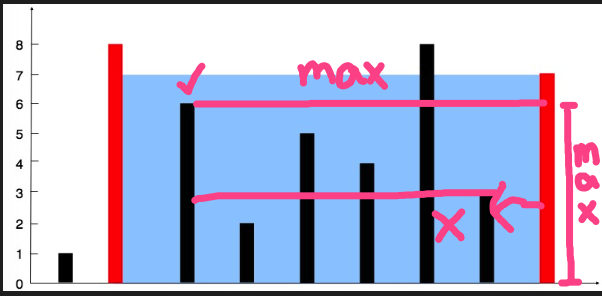
시간을 줄이기 위해서 리스트를 거꾸로 돌리고 break을 하는 방법을 사용했다. 넓이 = 가로 x 세로인데, 왼쪽 기준 기둥(첫 번째 if문)에서 가로가 가장 긴 맨 끝 기둥이 기준 기둥의 높이보다 크다면, 더 이상 가로 길이가 더 짧은 다음 기둥으로 옮길 필요가 없다. 왜냐하면 높이는 왼쪽 기준 기둥으로 고정되기 때문이다.
그런데도 time limit exceeded에 걸렸다.
class Solution:
def maxArea(self, height: List[int]) -> int:
ans = 0
def get_area(post1: List[int], post2: List[int]):
return abs(post2[0] - post1[0]) * (min(post1[1], post2[1]))
for idx1, h1 in enumerate(height):
for idx2, h2 in reversed(list(enumerate(height))):
if idx2 <= idx1:
break
if h1 < h2:
sub_ans = h1 * (abs(idx1 - idx2))
if sub_ans > ans:
ans = sub_ans
break
else:
sub_ans = get_area([idx1, h1], [idx2, h2])
if sub_ans > ans:
ans = sub_ans
return ans
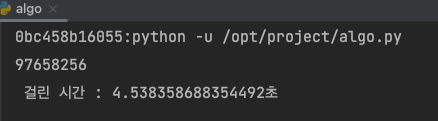
10000개가 들어있는 예제 리스트 기준, 로컬 컴퓨터에서 풀이 1은 약 28초, 풀이2는 약 4.5초가 걸렸다.
start = time.time()
result = Solution().maxArea(height)
end = time.time()
print(result)
print(f" 걸린 시간 : {end - start}초")
풀이3
Greedy 탐색 말고, Binary로 탐색해서 시간을 줄여보자는 생각에 다음과 같은 코드를 구상했다.
class Solution:
def maxArea(self, height: List[int]) -> int:
half_idx = round(len(height) / 2)
def get_area(post1: List[int], post2: List[int]):
return abs(post2[0] - post1[0]) * (min(post1[1], post2[1]))
def get_post(height: List):
best_post = [0, height[0]]
for idx, h in enumerate(height):
if idx == len(height) - 1:
candidate = [idx, h]
if candidate[1] > best_post[1] + (candidate[0] - best_post[0]):
best_post = candidate
return best_post
next_height = height[idx + 1]
if next_height > height[idx] + 1:
candidate = [idx + 1, next_height]
if candidate[1] > best_post[1] + (candidate[0] - best_post[0]):
best_post = candidate
post1 = get_post(height[:half_idx])
post2 = get_post(list(reversed(height[half_idx:])))
post2[0] = len(height) - post2[0] - 1
return get_area(post1, post2)
일단 절반으로 쪼개고, get_post를 2번 얻어와서 최종적으로 면적을 구하는 방식이다. 그리고 get_post 에서는 최고의 기둥? 을 구한다. '인덱스(가로길이)가 하나 커지는 것은 높이가 하나 줄어드는 것과 같다' 라는 컨셉으로 진행했다.
쉽게 테스트 코드들을 통과하는 듯 했지만, 아래 케이스에서 또 실패했다..
[1,2,4,3]
내 코드 기반으로 보면, [1,2,4] , [3] 두 개의 리스트로 나눠서 각각 최고의 기둥을 구한다. 1 -> 2로 갈 때, 가로너비가 1 줄어드는 것 대비, 높이가 똑같이 1밖에 증가 안하므로 최고의 기둥이 변경되지 않는다. 그러나 2 -> 4로 갈때는 가로 너비가 1 줄어드는 것 대비, 높이가 2 증가하므로 최고의 기둥은 4가 된다. 우측 리스트는 1개밖에 없으므로 3이 된다. 이 결과에 따르면 최종 면적은 가로 x 세로 = 1 x 3 = 3이 된다. 그러나 생각해보면, 2와 3을 이용하여 기둥을 구성하면 가로 x 세로 = 2 x 2 = 4가 되어 더 큰 면적이 나오게 된다...
좌절하지 말고 계속 천천히 생각해보자.
궁금했던 점 기록
- 어떻게 시간을 줄일 수 있을까?
4. 해법
- 힌트
- 링크
- 풀이 보기
참조
'Computer Science > Algorithm' 카테고리의 다른 글
| git으로 통합함 (0) | 2023.10.04 |
|---|---|
| [Leetcode] [미결] 10. Regular Expression Matching (0) | 2023.06.08 |
| [Leetcode] 9. Palindrome Number (0) | 2023.06.07 |
| [Leetcode] 8. String to Integer (atoi) (0) | 2023.06.03 |
| [LeetCode] 7. Reverse Integer (0) | 2023.06.02 |