primePassword
문제
다음의 조건을 만족하면서 현재의 비밀번호('curPwd')를 새 비밀번호(newPwd)로 변경하는 데 필요한 최소 동작의 수를 리턴해야 합니다.
- 한 번에 한 개의 숫자만 변경가능하다.
- 4자리의 소수(prime)인 비밀번호로만 변경가능하다.
정리하면, 비밀번호가 계속 소수를 유지하도록 숫자 한 개씩을 바꿔갈 때 현재 비밀번호에서 새 비밀번호로 바꾸는 데 최소 몇 개의 숫자를 변경해야 하는지를 리턴해야 합니다.
입력
인자 1 : curPwd
- number 타입의 1,000 이상 9,999 이하의 자연수
인자 2 : newPwd
- number 타입의 1,000 이상 9,999 이하의 자연수
출력
- number 타입을 리턴해야 합니다.
주의사항
- 4자리인 소수는 1,000 이상의 소수를 말합니다.(0011, 0997 등은 제외)
입출력 예시
let output = primePassword(1033, 1033); console.log(output); // --> 0 output = primePassword(3733, 8779); console.log(output); // --> 3 (3733 -> 3739 -> 3779 -> 8779)
풀이
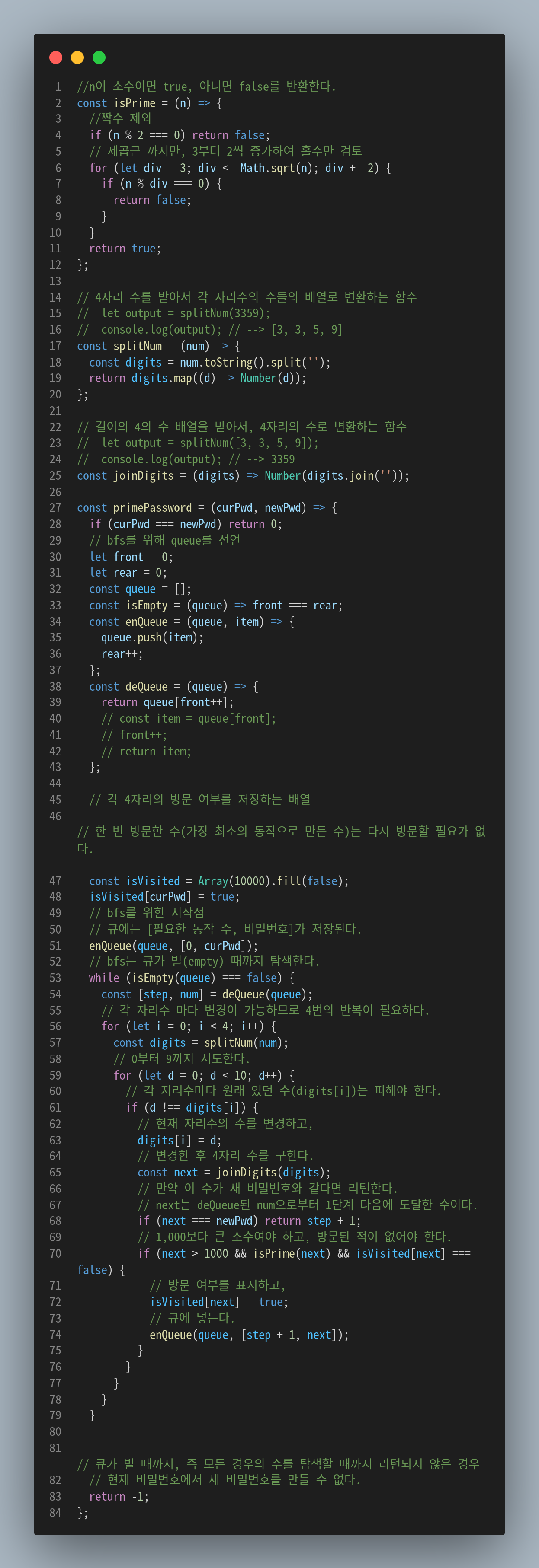
크게 세가지 개념을 사용한다고 볼 수 있겠다.
1. 소수 판별
2. 각 자리수를 type 변화를 통해 변환
3. queue
1. 소수 판별
소수 판별 함수는 예전 다른 글(소수 구하기 : isPrime, prime number, sqrt)에서 적은 것과 같이, 소수를 판별하고자 하는 n 값을 받아와서 모든 자연수로 나누어본다. 다만, sqrt(n) 까지만 나누고, 짝수는 제외한다.
2. 각 자리수를 type 변화를 통해 변환
각 자리수를 하나씩 더해야 한다. 그냥 생각하면 for문을 돌면서 +1 또는 +10, +100... 할 수 있겠으나 수가 커질수록 코드가 길어지게 된다. 따라서 splitNum, joinDigits 함수를 만들어서 사용한다. 이것은 숫자를 string으로 변환한 뒤에 split하여 배열로 만든 뒤, 배열의 각 요소를 더함으로써 가능하다.
.toString().split(''), map, Number, join('') 문법의 활용에 유의하자.
3. queue
BFS를 적용해서 curPwd 에서 newPwd로 가는 최소의 이동방법을 찾는다.
primePassword(3733, 8779) --> 3의 test case를 살펴보자.

우측 하단의 queue에 0~7의 index까지 쌓인 요소들을 살펴보면 어떤 방식으로 진행되는지 알 수 있다.
[0, 3733]을 대상으로 for문을 돌려서, next를 찾는다. 그리고나서 step과 다음단계의 숫자 next = 1733을 queue에 넣는다.
계속해서 [0, 3733]을 대상으로 모든 자릿수에 대해 검토하여 queue에 집어넣는다(BFS).
(한 가지 경우에 대해 모든 경우의 수를 검토하고 다음 단계(step = 0 에서 step = 1로)로 넘어가므로 BFS라 할 수 있겠다.
사진에는 안나와있지만, 이렇게 하고나서는 front = 0 이던 것이 front = 1이 될 것이고, [1,1733]을 대상으로 위의 과정을 반복할 것이다. 그때부터는 step = 2의 값을 갖는 값들이 queue에 순서대로 쌓이기 시작할 것이다.
일단 queue에는 step=1인 값들이 무수히 쌓여있으므로, 이 경우들을 모두 처리하면서 curPwd = newPwd인 경우를 찾고 만약 그 경우에 도달한다면 바로 step+1을 반환함으로써 답을 찾아내는 방식이다.
Test Case
primePassword(1033, 1033) --> 0
primePassword(3733, 8779) --> 3
primePassword(1009, 1171) --> 5
primePassword(9787, 9923) --> 6
'Computer Science > Algorithm' 카테고리의 다른 글
| Prm 17 : balancedBrackets / stack, in 연산자 객체 적용 (0) | 2021.01.11 |
|---|---|
| quickSort / 퀵정렬 (0) | 2021.01.10 |
| 소수 구하기 : isPrime, prime number, sqrt (0) | 2021.01.09 |
| Prm 14 : rotatedArraySearch / binarySearch, 경우의 수 (0) | 2021.01.08 |
| insertionSort / 삽입정렬 (0) | 2021.01.08 |


