가장 기본적인 게이트들의 조합을 통해 우리 세상에 필요한 기본적인 기능을 갖춘 중간 규모 집적 회로(MSI, medium-scale integration)을 만들 수 있다. 이런 부품들의 조합을 통해 대규모 집적회로(LSI, large-scale integration), 초대규모 집적 회로(VLSI, very large-scale integration) 등을 만들 수 있다.
논리식의 간소화
다양한 집적회로들을 공부하기 전에, 논리식을 간소화하는 방법부터 배워본다. 여러 게이트들을 집적했을 때 입력에 따라 출력값이 어떻게 나오는지 알기 위해서는 이 내용을 알고 있어야 한다.

불함수를 간략화하는 일반적인 규칙들은 다음과 같다.
1. A x 1 = A 이다. A가 0이면 0 x 1 = 0이고, A가 1이면 1 x 1 = 1이기 떄문이다. (x는 and를 의미)
2. A + 1 = 1 이다. +는 OR를 의미하므로 1 OR 1 = 1, 0 OR 1 = 1 이다.
3. AA = A 이다. A가 아무리 많더라도 1 x 1 x 1... = 1, 0 x 0 x 0 ... = 0 이다.
4. A + BC = (A + B) x (A +C)이다.
5. A + A' = 1이다. 1 or 0 이거나 0 or 1 은 1이기 때문이다.
6. AA' = 0이다. 1 and 0 = 0
카르노맵
카르노맵은 많은 수의 부울변수(예를 들었던 A, B처럼 0과 1만 존재하는 변수)가 있을 때도 간편하게 도식화할 수 있는 표현 방법이다.
예시 1)

그림대로 A, B, A', B'을 표기하되, 중간 네모에 1로 표시된 부분은 사각형으로 묶어준다. 다만 연속적으로 표시된 부분만 묶는다. 그리고 1, 2, 4, 8, 16, ... 등과 같이 2의 배수의 크기로만 묶는다.
세로로 된 직사각형 부분을 본다. 직사각형의 좌측에 A와 A'이 해당된다. 이렇게 A, A' 모두 해당되면 무시한다. 직사각형의 위쪽에 B'이 해당된다. 따라서 세로로 된 직사각형의 결과는 B' 이다.
가로로 된 직사각형 부분을 본다. 위 세로로 된 직사각형의 원리와 같이 생각해보면 결과는 A'이다.
두 직사각형의 결과를 +로 더한다. 그럼 A'+B'가 최종 결과가 되며 이것은 아래 수식과 같이 표현할 수 있다.

예시 2)

그레이코드
이제 부울변수가 3개인 경우이다. 세로 변이 A, 가로변이 BC로 표기되어있다. 여기서 유의할 점은 BC의 바이트표현식이 그레이코드로 작성되어있다는 것이다. 다시 말해 이진수의 크기 순서대로라면 00, 01, 10, 11일 것이 순서가 바뀌어서 표현되었다. 이 그레이코드는 원래의 크기순으로 나열된 이진수에 맨 첫자리를 제외하고 XOR를 적용해보면 된다. XOR은 두 비트가 다를때만( 3개 비트일때는 1개가 참일때만) 참이다. 방법은 아래 그림과 같다(참조2)
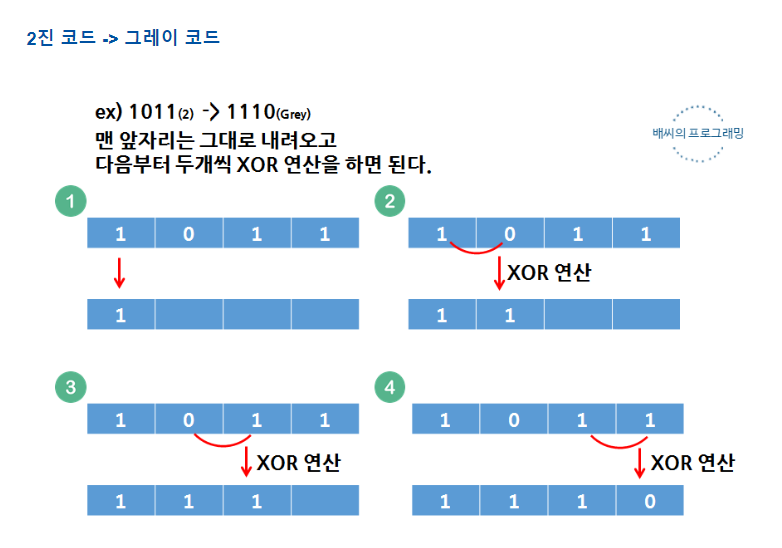
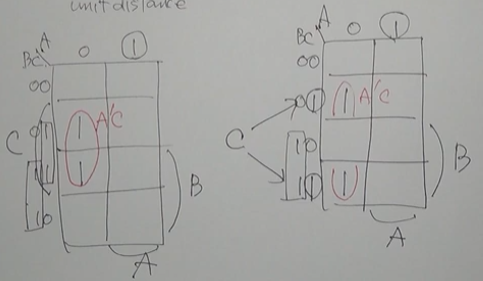
그레이 코드로 작성하는 이유는, 카르노 맵을 만들 때 1이 붙어있도록 설계하기 위함이라고 한다. 참조 3의 그림을 보면 대략적으로는 이해가 된다. 다만 이것까지 깊이 이해하는건 다음에 필요할 때 하자.
결과 구해보기
이제 사각형으로 묶으면 된다. 다만 사각형은 클수록 논리식을 간소화하기가 편하다는 것도 기억하자.

-왼쪽 위 사각형
좌측은 A' 확정, 상단은 B'은 중복되고 C' 및 C가 있어 C는 무효항이된다. 1개의 사각형에서 결과는 AND 연산하면 된다. 따라서 A'B'이 된다.
-오른쪽 아래 사각형
좌측은 A 확정, 상단은 B이다. 따라서 AB가 된다.
-처음과 끝에 걸친 사각형
좌측은 A, A'에 해당하므로 무효항이 된다. 상단은 C'만 남는다. 따라서 C'이 된다.
--결과
각 사각형의 결과들을 더하면 A'B' + AB + C'이다.
참조
0. [책] 한 권으로 읽는 컴퓨터 구조와 프로그래밍
1. 길벗 시나공 IT 강의
https://www.youtube.com/watch?v=W1xc4tDICMc
2. 배씨의 프로그래밍 블로그
3. Youtube - 뽕교수의 논리회로
'Computer Science > Introduction' 카테고리의 다른 글
| 9. [종합][스터디] 드 모르간의 법칙, 2의 보수, UTF-8, Base64 인코딩 이유 (0) | 2022.04.27 |
|---|---|
| 8. 가산기, 디코더/인코더, 멀티플렉서/디멀티플렉서 (0) | 2022.04.19 |
| 6. (보충) 출력유형 : Open Collector, Push Pull, Totem Pole (0) | 2022.04.17 |
| 5. 이력현상, 차동신호, 전파지연 (0) | 2022.04.10 |
| 4. 비트처리 하드웨어 : 릴레이, 진공관, 트랜지스터, 논리게이트 (0) | 2022.04.10 |



